Relationship Between Current And Resistance When Voltage Is Constant
Relationship Between Current And Voltage When A Resistor Follows Ohm S Law Gcse Physics Science Revision Ohms Law
State And Explain Ohm S Law Formula Voltage Current And Resistance Ohms Law Ohms Electrical Projects
Dc Circuit Theory With Images Circuit Theory Dc Circuit Ohms Law
V I And R Relationship Circuit Theory Dc Circuit Ohms Law
Voltage Current Resistance And Ohm S Law Ohms Law Ohms Paper Circuits
Ohms Law Ohms Law Electronics Basics Electrical Projects
Where i is the current through the conductor in units of amperes v is the voltage measured across the conductor in.
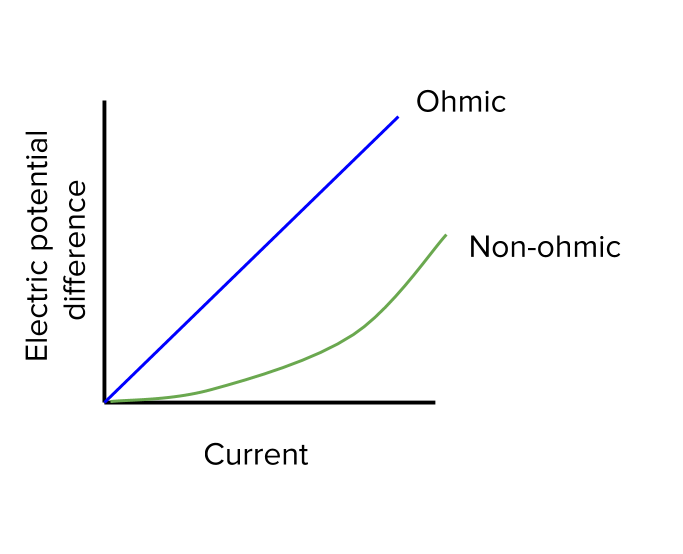
Relationship between current and resistance when voltage is constant. For a constant resistor if the voltage across it remains unchanged the current through it remains unchanged. The amount of electric current through a metal conductor at a constant temperature in a circuit is proportional to the voltage across the conductor and can be described by. In a linear circuit of fixed resistance if we increase the voltage the current goes up and similarly if we decrease the voltage the current goes down. For linear devices ohm s law is being followed and this law is not applicable on non linear devices.
Ohm s law states. This states that the current flowing in a circuit is directly proportional to the applied voltage and inversely proportional to the resistance of the circuit provided the temperature remains constant. Ohm s law states that the current through a conductor between two points is directly proportional to the voltage across the two points. Relationship between voltage and resistance is different for two kinds of devices namely linear devices and non linear devices.
Ohm s law is certainly used in the electronics which is very powerful law. An important relationship between the current voltage and resistance in a circuit was discovered by georg simon ohm and it is called ohm s law. This means that if the voltage is high the current is high and if the voltage is low the current is low. Similarly if the voltage increases the current increases.
The relationship between voltage current and resistance forms the basis of ohm s law. The fundamental relationship between resistance voltage and current can be expressed using ohm s law. The relationship between resistance current and voltage is called as ohm s law. The relationship between current voltage and resistance is expressed by ohm s law.
Introducing the constant of proportionality the resistance one arrives at the usual mathematical equation that describes this relationship. Decreases the current also decreases.
Electric Potential Difference And Ohm S Law Review Article Khan Academy
The Ohm S Law Is A Basic Start For Those Who Want To Learn The Electrical Science Ohms Law Electronic Technician Electronics Education
How To Use A Multimeter To Measure Voltage Current And Resistance Root Mean Square Multimeter Electrical Wiring Diagram
Series And Parallel Circuits Explained Voltage Current Resistance Physics Ac Vs Dc Ohm S Law Youtube
Electric Current Electric Power Electrical Voltage Electricity And Electric Charge Potencia Eletrica Truques De Matematica Eletricidade Basica
How Voltage Current And Resistance Relate Ohm S Law
High School Physics Worksheet Questions Answers Resistance Ohm S Law Physics High School Worksheets Free Online Learning
Voltage Current Characteristics Of P N Junction Diode Knee Voltage Amp Zener Voltage In Hindi Youtube Hindi Video Resistance
Resistance And Resistors Boundless Physics
Tj Ohm S Law States That The Current Through A Conductor Between Two Points Is Directly Proportional Ohms Law Electrical Engineering Humor Electronics Basics
Ohm S Law Lab Physics 12 Portfolio Project
What Is The Relation Between Current And Voltage Quora
State And Explain Ohm S Law Formula Voltage Current And Resistance Ohms Law Ohms Materials Engineering
